Aggregated Selective Match Kernel

We introduce a framework to bridge the gap between the "matching-based" approaches, such as HE, and the recent aggregated representations, in particular VLAD. We introduce a class of match kernels that includes both matching-based and aggregated methods for unsupervised image search. We then discuss and analyze two key differences between matching-based and aggregated approaches. First, we consider the selectivity of the matching function, i.e., the property that a correspondence established between two patches contributes to the image-level similarity only if the confidence is high enough. It is explicitly exploited in matching-based approaches only. Second, the aggregation (or pooling) operator used in BoW, VLAD or in the Fisher vector, is not considered in pure matching approaches such as HE. We show that it is worth doing it even in matching-based approaches and that it tackles the burstiness phenomenon. This leads us to conclude that none of the existing schemes combines the best ingredients required to achieve the best possible retrieval quality. As a result, we introduce a new method that exploits the best of both worlds to produce a strong image representation and its corresponding kernel between images. It combines an aggregation scheme with a selective kernel. This vector representation is advantageously compressed to drastically reduce the memory requirements, while also improving the search efficiency.

We build a common model which can describe both matching based and aggregated methods. Both already existing methods and our proposed ones are described by this model. We propose the selective match kernel (SMK) and its aggregated counterpart (ASMK), which both use full precision residual vectors for local feature representation. Finally, this representation is binarized in the corresponding binary models SMK* ans ASMK* which allows the search to scale up to larger databases.

Matching features with descriptors assigned to the same visual word and similarity above the threshold. Examples for different values of the distance threshold and the selectivity parameter of our selective function. Color denotes descriptor similarity defined by the selective function, with yellow corresponding to 0 and red to the maximum similarity per image pair. The effect of the selective function is shown. A larger selectivity drastically down-weights false correspondences. This advantageously replaces hard thresholding as initially proposed in the Hamming Embedding method.

Examples of features mapped to the same visual word, finally being aggregated. Each visual word is drawn with a different color. Top 25 visual words are drawn, based on the number of features mapped to them. When relatively small vocabularies are used (as in VLAD) a lot of divergent features are aggregated. With larger vocabularies (as in our methods) aggregatation is applied on features which are commonly detected on repeated structures, thus tackling bustiness.

We evaluate the proposed methods on 3 publicly available datasets, namely Holidays, Oxford Buildings and Paris. We present experiments for measuring the impact of the parameters, and finally compare our methods against state-of-the-art methods. Evaluation measure is the mean Average Precision (mAP).

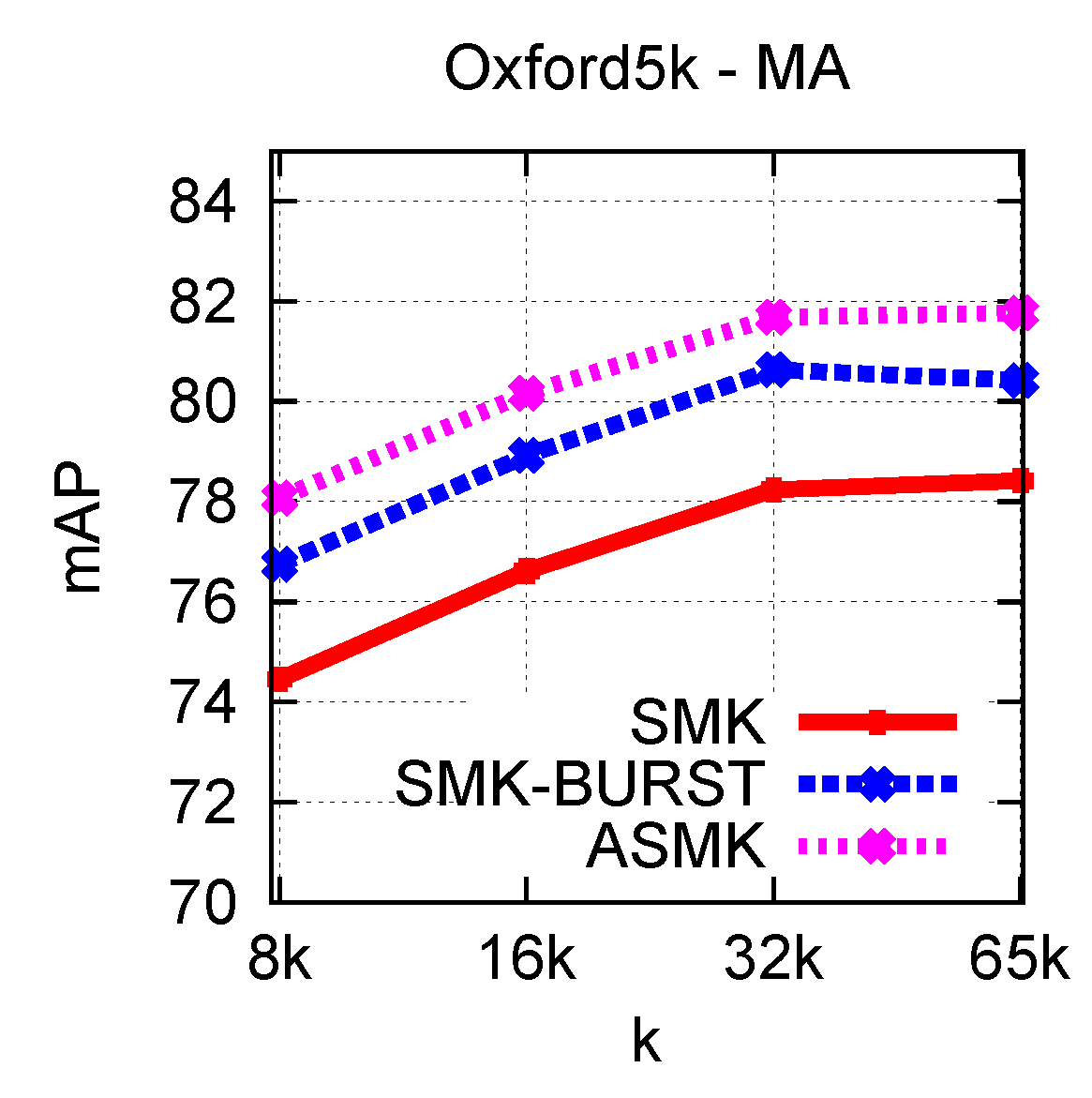
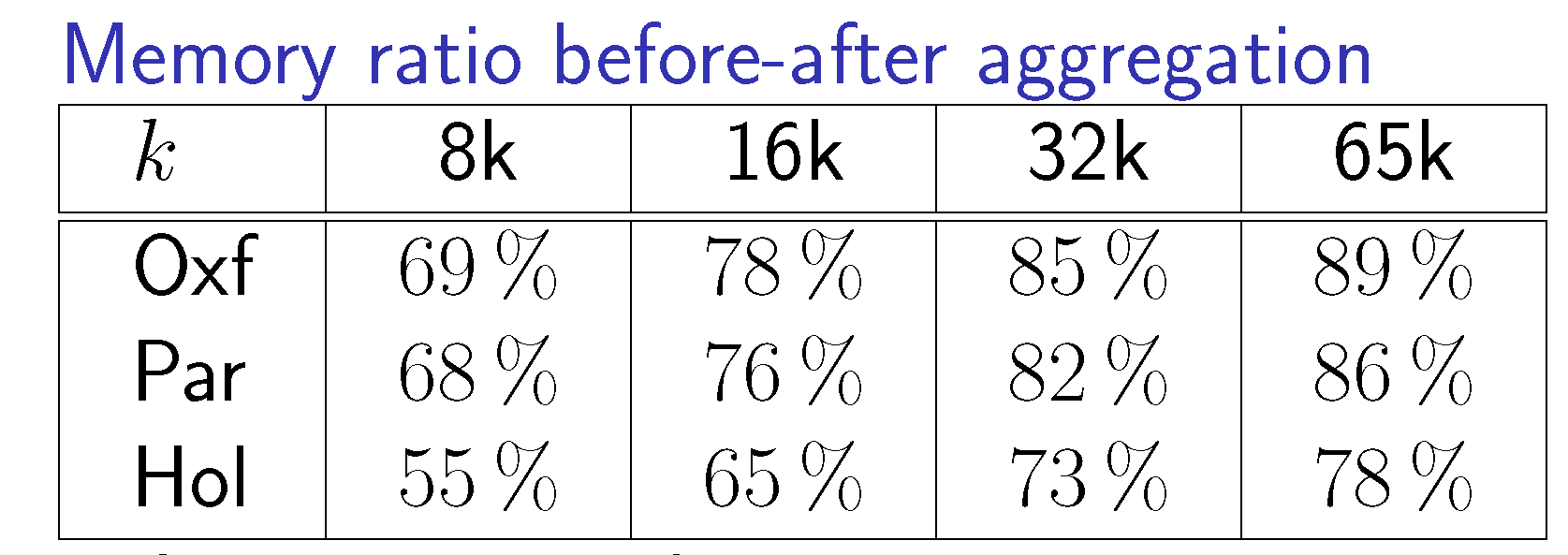
Source code is available here for the binarized method ASMK*.