Despite the success of the bag-of-words model in order to boost performance at large scale, geometry is still essential. Even if weaker or stronger geometric models are feasible in tasks like registration or recognition, this is clearly not the case for image retrieval. State of the art approaches are still based mostly on appearance in the filtering stage, while geometric or spatial constraints typically come as a second, re-ranking stage. Even in more recent work, this has only been achieved in the form of weak geometric constraints, or local geometry. On the other hand, global geometry indexing is at least as old as geometric hashing. To our knowledge, no work has been reported that can index appearance and global geometry for large scale image retrieval. This is exactly our attempt in the present work.

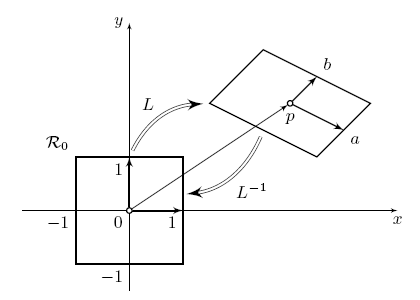
Figure 1. Normalization of a patch. A local feature is associated with a image patch L, which also stands for an affine transform.

We represent local image feature either as a patch or an affine transformation as shown in Figure 1. We extrapolate this transformation to the entire image frame, rectify the entire set of features and study image alignment via single correspondences between local features. We adopt a joint visual and spatial codebook and quantize the entire set of rectified local features into what we call a feature map. There is a feature map for each local feature and we can interpret it as a local descriptor, that encodes the global feature set rectified in a local coordinate frame. Well aligned feature sets of different but similar images are likely to have maps with a high degree of overlap.

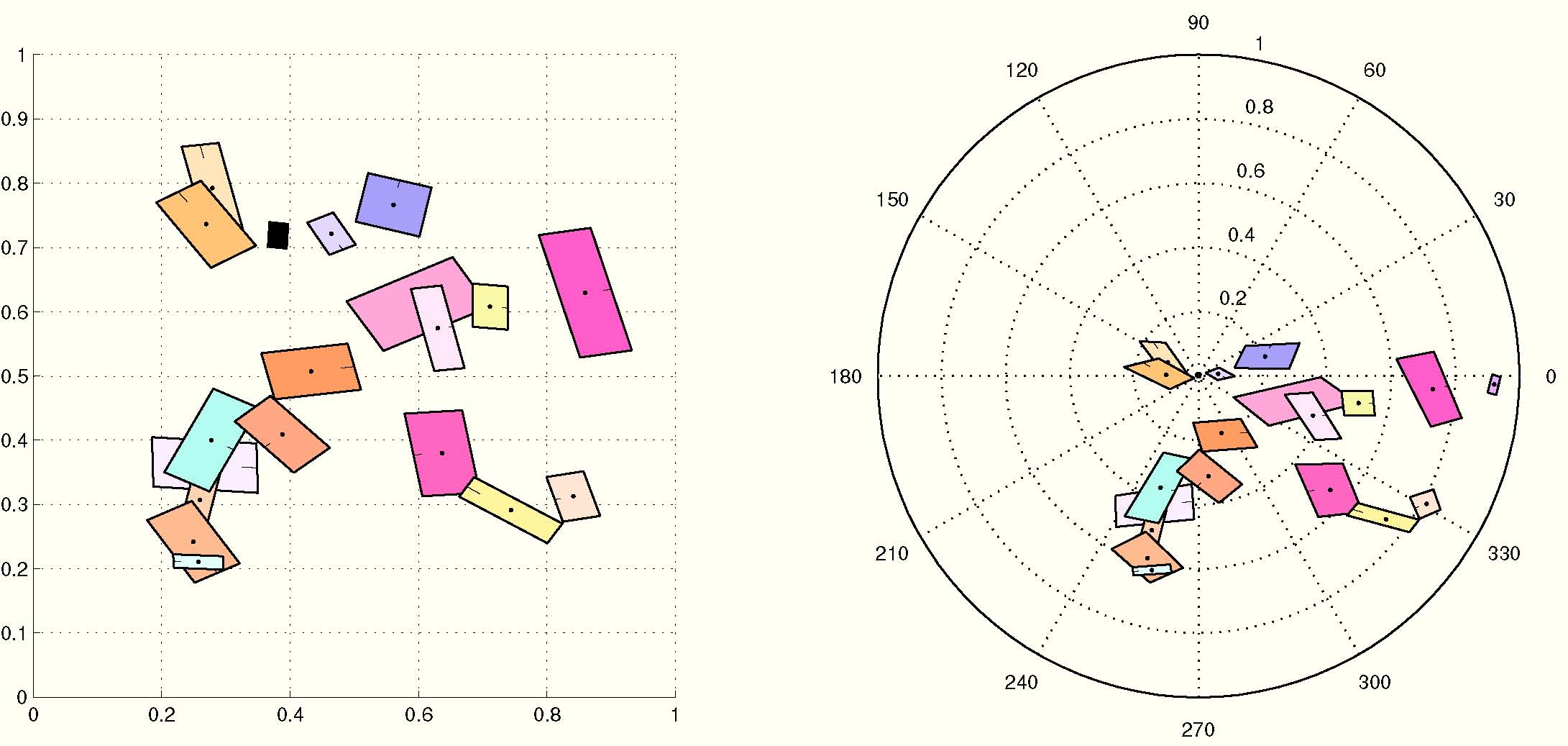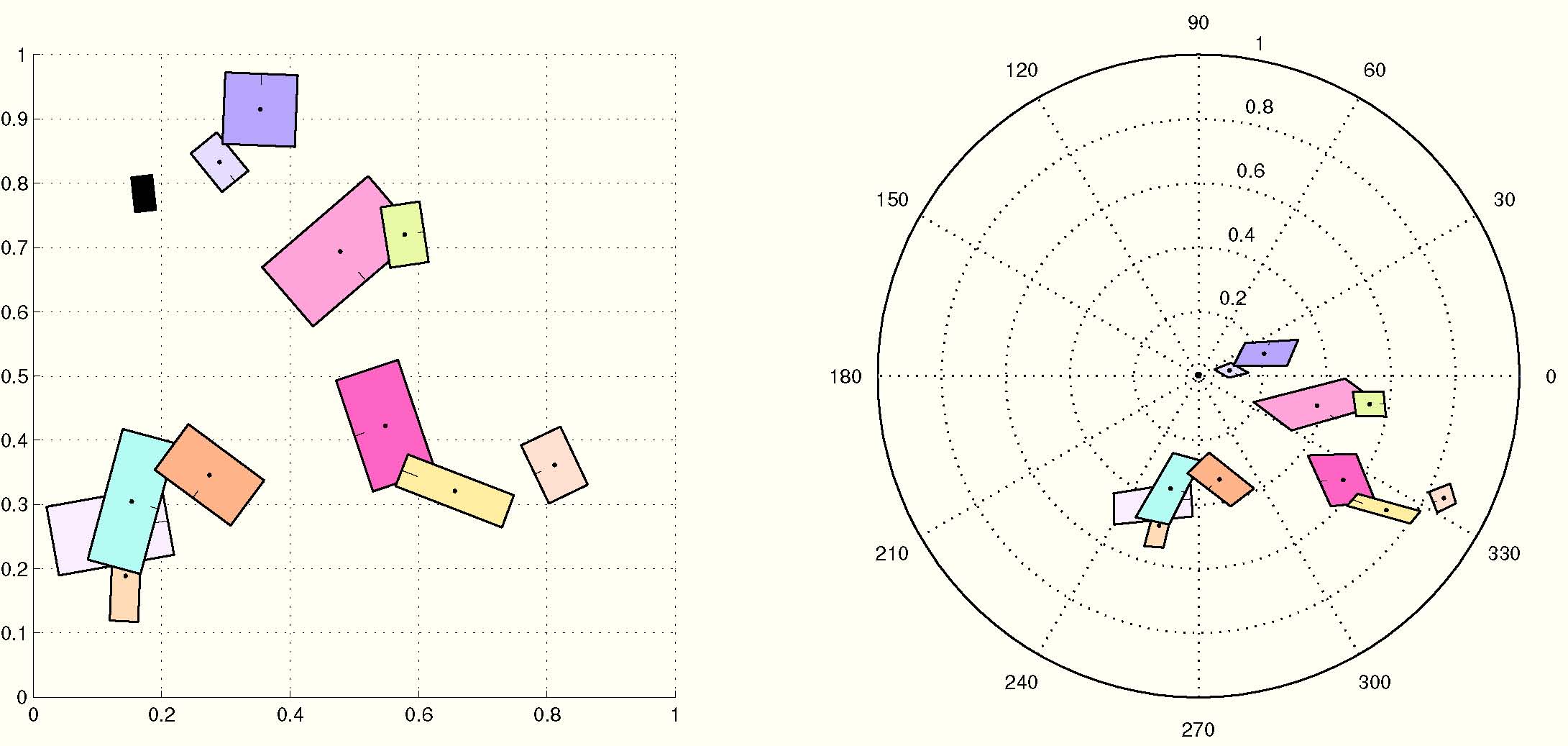
Figure 2. Left: A random set of patches and the rectified counterpart. Right: The same set of random patches under affine transform where patch position and local shape are distorted and the corresponding rectified set. Origins are the two black patches in both sets.

Figure 2 shows a random feature set, a transformed and distorted version, and the rectified counterparts with their origins in correspondence. Notice how the latter are roughly aligned. We define a feature map similarity (FMS) as the intersection between the joint histograms (spatial and visual). Each non zero term is associated to correspondences between feature sets as depicted in Figure 3. Likewise, Figure 4 depicts inliers between real images. For comparison it also depicts inliers found using Fast Spatial Matching (FastSM) of [Philbin et al. CVPR 2007].

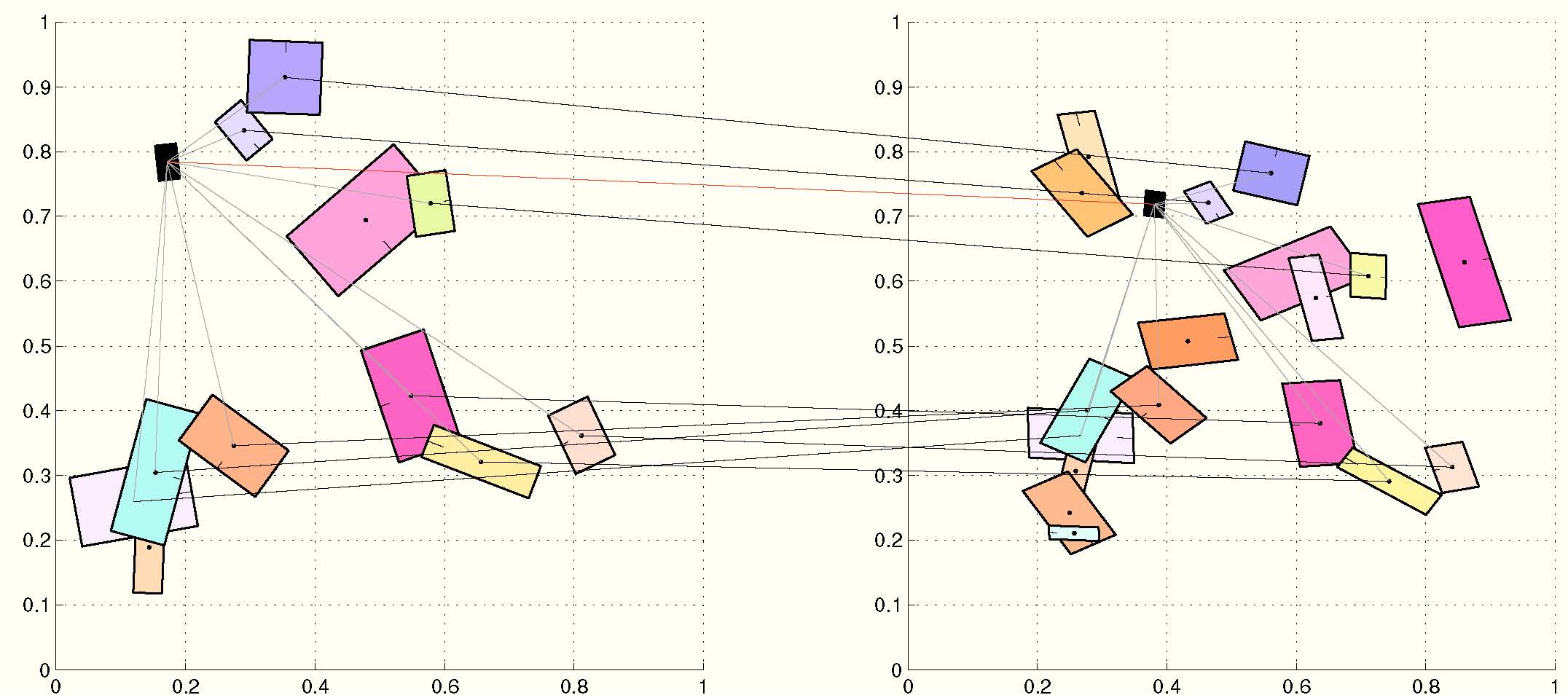
Figure 3. Inliers between two sets of features using FMS. Black lines connect inliers. Red line connects the origins. Grey lines connect origins with inlier features.

Figure 4. Above: Inliers using FastSM. Below: Inliers using FMS. There are 35 and 32 inliers respectively. Correspondences between inliers are show in yellow color. Origins are shown in red circles with scale and rotation.

Starting with an image representation by a collection of feature maps. We extend min-wise independent permutations to collections of sets and derive a similarity measure for such collections. Finally, we exploit the sparseness of our representation and build an inverted file structure, which incorporates both appearance and geometry of an image. Query time is sub-linear in the total number of images, ideally linear in the number of relevant ones.

We have conducted experiments on two publicly available datasets, namely Oxford Buildings and INRIA Holidays, as well as on our own European Cities dataset which will be soon available in our datasets website. The latter is particularly challenging because distractors urban scenes exactly like the ground-truth set. We compare the proposed approach with retrieval using bag-of-words (BOW) [Sivic and Zisserman CVPR 2003] and weak geometric consistency (WGC) [Jegou et al. ECCV 2008]. Comparisons are also performed when using spatial verification with all the methods. FMH outperforms other methods especially in the presence of a large number of distractors.

Table 1. Mean average precision for INRIA Holidays and Oxford Buildings datasets, with and without distractors. FastSM is performed on the 100 top-ranked results; LO on both 100 and 1000 top-ranked results. Outperforming method shown in boldface.

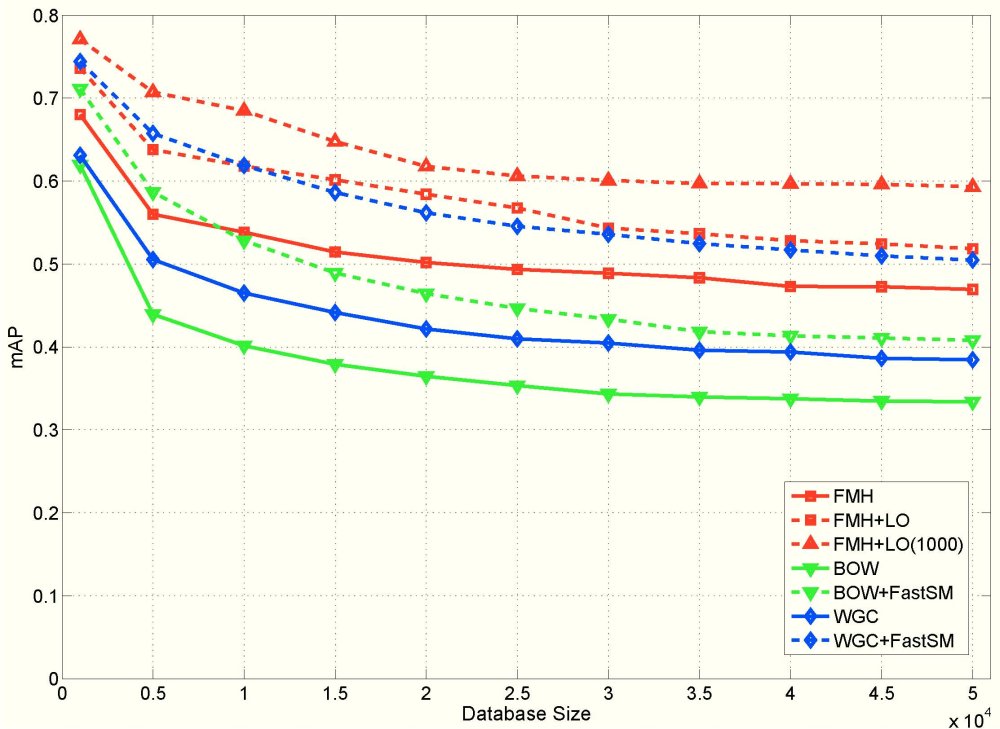
Figure 5. Mean average precision for varying database sizes on the European Cities dataset for BoW,WGC and FMH, with and without re-ranking.

To our knowledge, the present work is the first to integrate appearance and global geometry in sub-linear image indexing, while being invariant to affine transformations and robust to occlusion. We consider our experiments successful because we make partial matching work at large scale, and demonstrate how this keeps precision almost unaffected under a significant amount of distractors.

We have developed our methodology for affine transformations, and this is because state of the art feature detectors are affine covariant. Extending e.g. to homography would be straightforward, should such features mature. We consider the feature map representation the most important contribution of this work. We foresee a new research direction in applying this concept to problems like large scale object recognition and detection, where geometric consistency and invariance are as crucial as in retrieval.