 IVA
IVA Locally Optimized Product Quantization
We present a simple vector quantizer that combines low distortion with fast search and apply it to approximate nearest neighbor (ANN) search in high dimensional spaces. Leveraging the very same data structure that is used to provide non-exhaustive search,
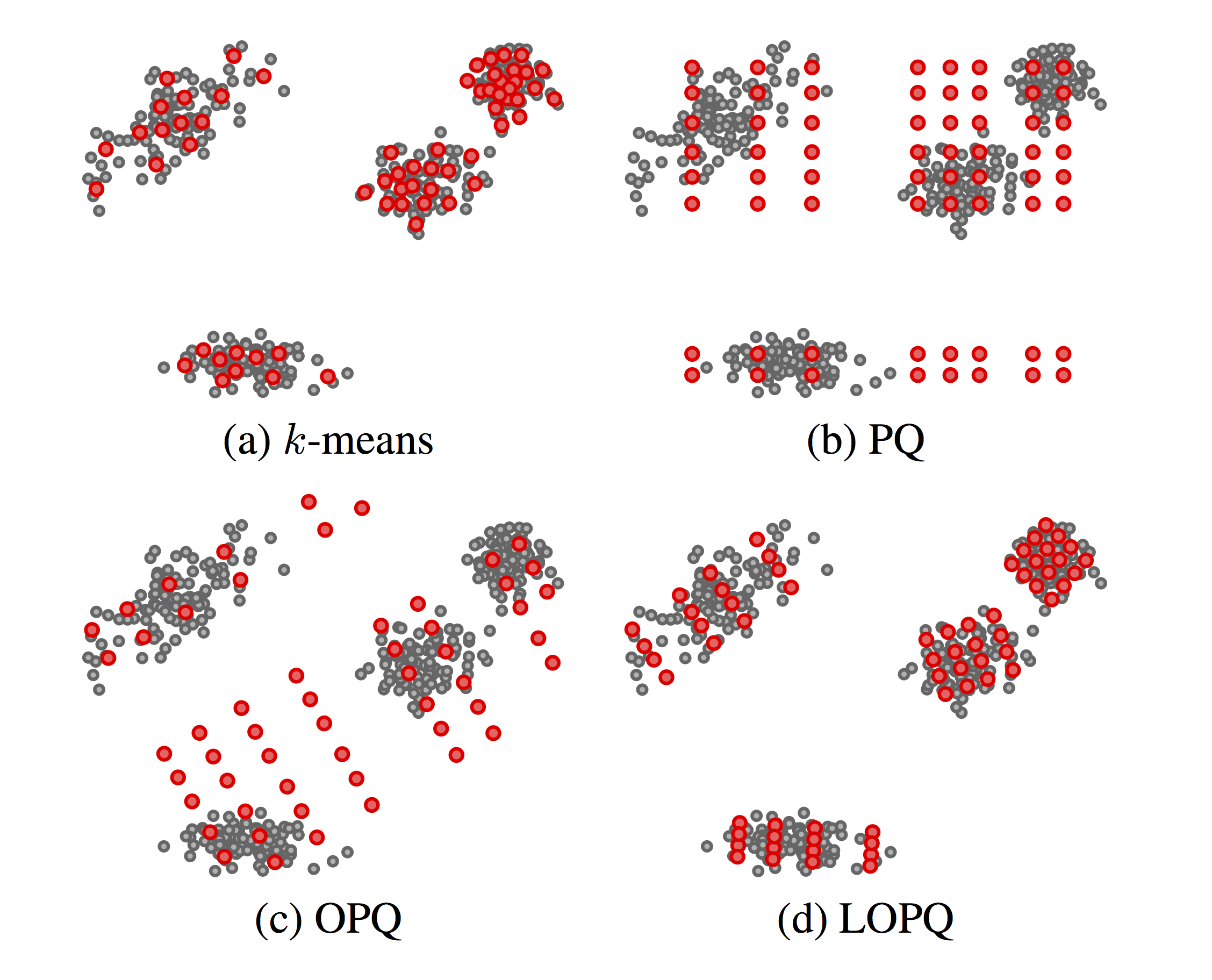 |
Figure 1. Four quantizers of $64$ centroids each, trained on a random set of 2D points, following a mixture distribution. (c) and (d) also reorder dimensions, which is not shown in 2D |
$K$-means, depicted in Fig. 1(a), is a vector quantization method where by specifying $k$ centroids, $\log_2 k$ bits can represent an arbitrary data point in $\mathcal{R}^d$ for any dimension $d$; but naive search is $O(dk)$ and low distortion means very large $k$. By constraining centroids on an axis-aligned, $m$-dimensional grid, Product Quantization (PQ) [1] achieves $k^m$ centroids keeping search at $O(dk)$; but as illustrated in Fig. 1(b), many of these centroids remain without data support, e.g. if the distributions on $m$ subspaces are not independent.
Optimized Product Quantization (OPQ) [2] allows the grid to undergo arbitrary rotation and re-ordering of dimensions to better align to data and balance their variance across subspaces to match bit allocation that is also balanced. But as shown in Fig. 1(c), a strongly multi-modal distribution may not benefit from such alignment.
Our solution in this work is locally optimized product quantization (LOPQ). Following a quite common search option, a coarse quantizer is used to index data by inverted lists, and residuals between data points and centroids are PQ-encoded. But within-cell distributions are largely unimodal; hence, as in Fig. 1(d), we locally optimize an individual product quantizer per cell. Under no assumptions on the distribution, practically all centroids are supported by data, contributing to a lower distortion.
- Vector quantization: Minimize distortion $E = \sum_{\mathbf{x} \in \mathcal{X}} \| \mathbf{x} - q(\mathbf{x}) \|^2$, where quantizer $q : \mathbf{x} \mapsto q(\mathbf{x}) = \arg\min_{\mathbf{c} \in \mathcal{C}} \| \mathbf{x} - \mathbf{c} \|$.
- Product quantization [1]: $\mathcal{C} = \mathcal{C}^1 \times \dots \times \mathcal{C}^m$, i.e.: $k^m$ centroids of the form $\mathbf{c} = (\mathbf{c}^1, \dots, \mathbf{c}^m)$ with each sub-centroid $\mathbf{c}^j \in \mathcal{C}^j$ for $j \in \mathcal{M} = \{ 1, \dots, m \}$. $m$ independent sub-problems: $q(\mathbf{x}) = (q^1(\mathbf{x}^1), \dots, q^m(\mathbf{x}^m))$.
- Optimized product quantization [2]: $\mathcal{C} = \{ R\hat{\mathbf{c}} : \hat{\mathbf{c}} \in \mathcal{C}^1 \times \dots \times \mathcal{C}^m, R^{T}R = I\}$, where orthogonal $d \times d$ matrix $R$ optimized for subspace decomposition (rotation + permutation).
[1] Jegou et al.. Product quantization for nearest neighbor search. PAMI, 2011.
[2] Ge et al.. Optimized product quantization for approximate nearest neighbor search. CVPR, 2013.
[3] Babenko and Lempitsky. The inverted multi-index. CVPR, 2012.
- Locality: Partitioning data in cells with a coarse quantizer of $K$ cells, we locally optimize one product quantizer per cell on the residual distribution.
- Efficient training: Local distributions are easier to optimize via a simple OPQ variant.
- Multiple search frameworks: Fits naturally to either a single or a multi-index [3].
- Product optimization: For an $n^{\mathrm{th}}$-order multi-index, we only optimize $nK$ product quantizers for a total of $K^n$ cells.
If $\mathcal{Z}$ is the set of residuals of data points quantized to some cell and $|\mathcal{C}^j| = k$ for $j \in \mathcal{M} = \{ 1, \dots, m \}$, we locally optimize both space decomposition and sub-quantizers per cell, using OPQ: % \begin{equation} \begin{array}{rl} \mathrm{minimize} & {\displaystyle \sum_{\mathbf{z} \in \mathcal{Z}} \min_{\hat{\mathbf{c}} \in \hat{\mathcal{C}}} \| \mathbf{z} - R\hat{\mathbf{z}} \|^2} \\ \mathrm{subject\ to} & \hat{\mathcal{C}} = \mathcal{C}^1 \times \dots \times \mathcal{C}^m \\ & R^{T}R = I, \end{array} \label{eq:opt} \end{equation}
Parametric solution: Assuming a normal distribution, minimize the theoretical lower distortion bound as a function of $R$ alone via PCA alignment and eigenvalue allocation. Sub-quantizer optimization follows as in PQ.
Residual distributions are closer to normal, so parametric solution fits better to LOPQ.
- Single index: For each of $K$ cells, residual is individually rotated and encoded. The query point is soft-assigned to its $w$ nearest cells. Asymmetric distances are computed exhaustively via lookup tables.
- Multi-index: Two subspace quantizers $Q^1, Q^2$ of $K$ centroids each are built. Residuals are encoded per row and column: $2K$ local rotations and sub-quantizers for a total of $K^2$ cells. Search follows multi-sequence algorithm, with lazy evaluation of row/column-rotated query residuals.
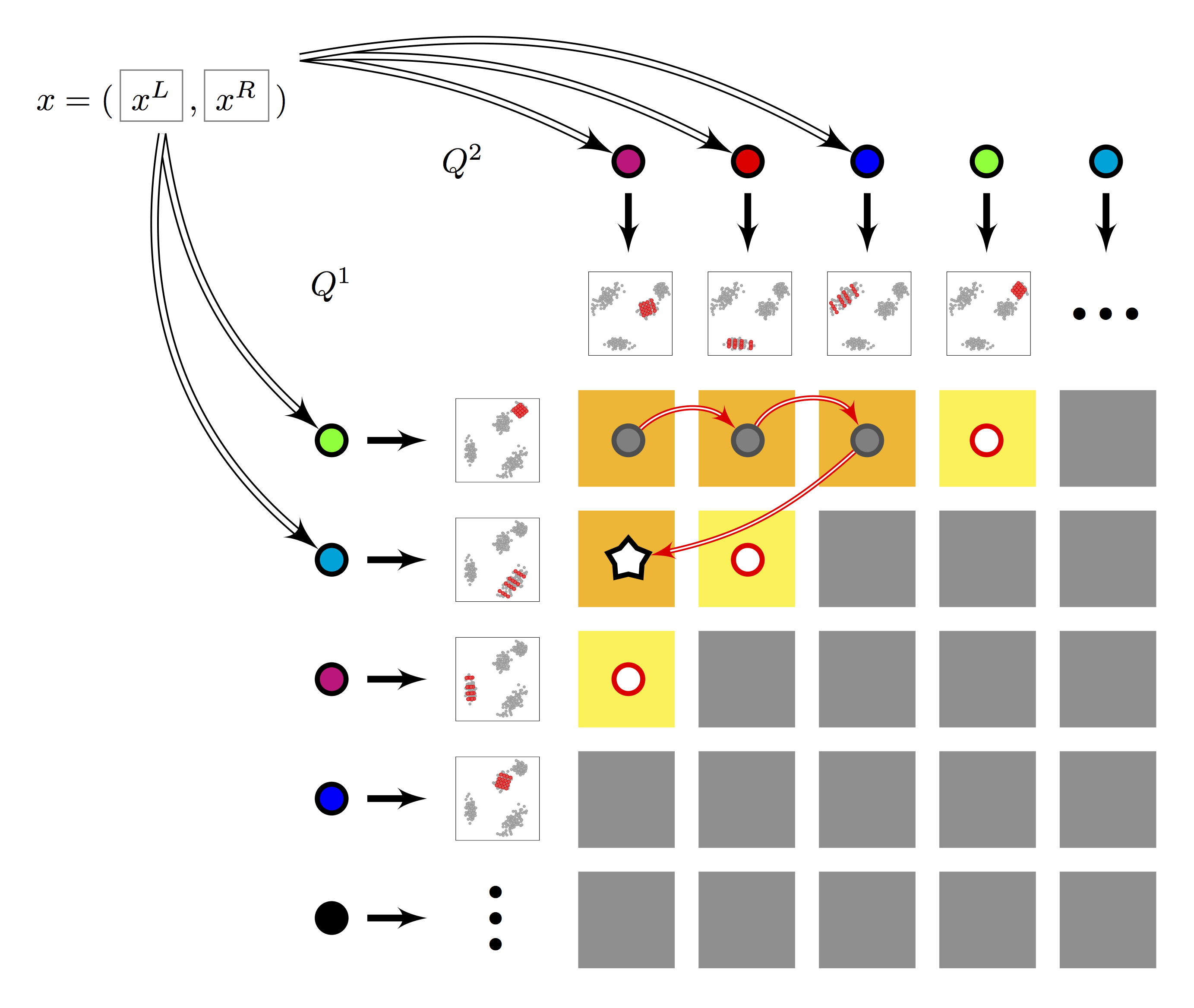 |
Figure 2. Multi-LOPQ |
 |
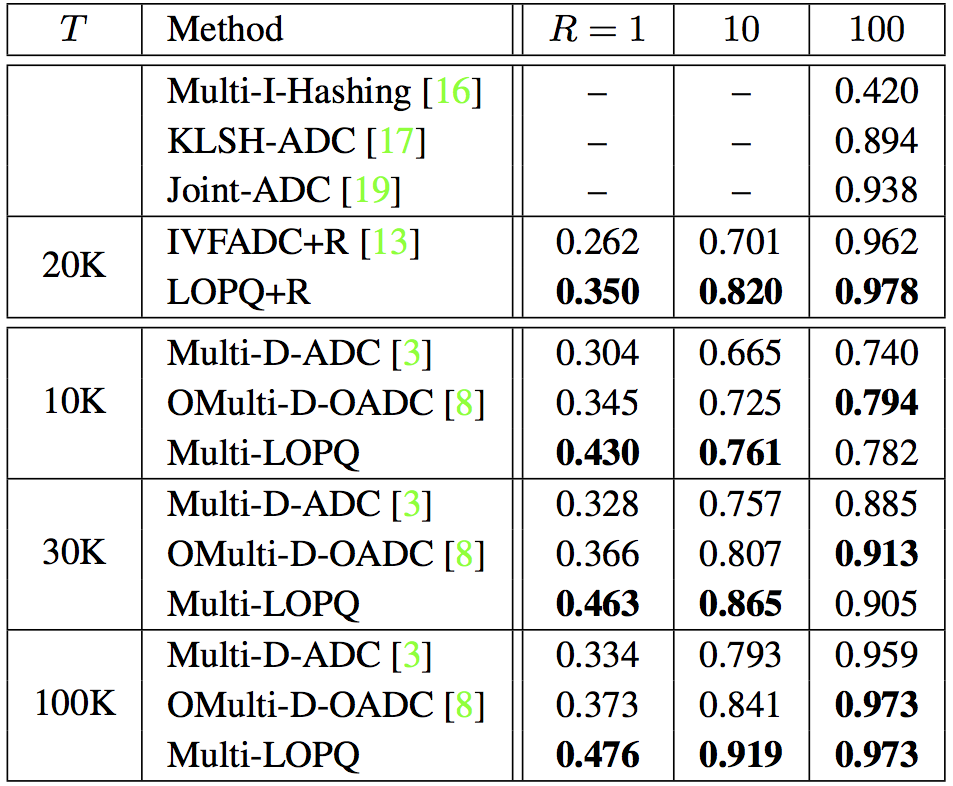 |
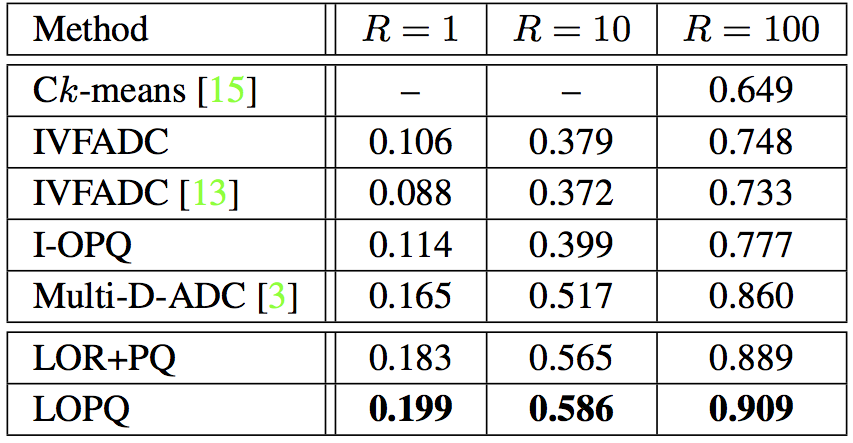
SIFT1B with $64$-bit codes, $K = 2^{13} = 8192$ and $w=64$. For Multi-D-ADC, $K = 2^{14}$ and $T=100$K. |
SIFT1B with $128$-bit codes and $K = 2^{13} = 8192$ (resp. $K = 2^{14}$) for single index (resp. multi-index). For IVFADC+R and LOPQ+R, $m'=8$, $w=64$. & |
Overhead on top of IVFADC (resp. Multi-D-ADC):
- Space: $Kd^2$ (resp. $2K(d/2)^2$) for rotation matrices, i.e. around 500MB on SIFT1B and $Kdk$ for sub-quantizers, i.e. 2GB on top of 21GB for SIFT1B.
- Query time:The time needed to rotate the query for each soft-assigned cell (row/column). Average overhead on SIFT1B for Multi-LOPQ is $0.776$, $1.92$, $4.04$ms respectively for $T=10$K, $30$K, $100$K.
Optimized source code for LOPQ is not publicly available. All resources found below are for demonstrative purposes and do not follow the exact search methodology presented in the paper. For fast and scalable ANN search with LOPQ, one may modify Artem's excellent implementation of the inverted multi-index.
Source code in MATLAB and C++ can be found here. This code is for demonstrative purposes only. Precomputing projections for all queries is only done to facilitate parameter tuning and is suboptimal.
Source code in Python with distributed training in Spark can be found here.
Conferences
[ Abstract ] [ Bibtex ] [ PDF ] [ Poster ]