ivl

the problem

This is a non-trivial problem with a simple solution that can be programmed in a few lines of code, illustrating several ivl features. Imagine we have two sets of points on a plane, represented by small circles and crosses, respectively. The points in the two sets are more or less the same, apart from a geometric transformation. For instance, translation + scaling (left), or rotation (right):

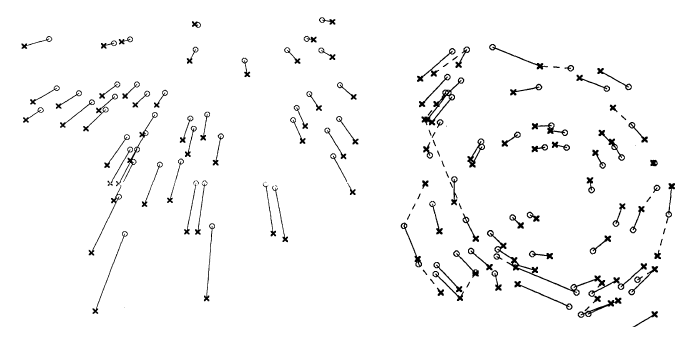
As shown here, we would like to connect each circle to a nearby cross, in order to capture the apparent motion from the one set of points to the other. Here is a more formal definition of the problem:

• given two sets of points $a_i, i = 1,\dots,m$ and $b_j, j = 1,\dots,n$ on the same plane, let $d_{ij}$ be the distance between $a_i$ and $b_j$
• then, the problem is to find an one to one mapping from as many as possible points $a_i$ to $b_j$ such that the sum of squared distances between corresponding points is minimized

This problem is harder than standard least squares because the set of feasible solutions is discrete.

the solution

A simple approximate solution was given in 1991 by Scott and Longuet-Higgins in An Algorithm for Associating the Features of Two Images. Will we not explain why, but the solution goes as follows, in four steps.

[don't bother if all this does not mean much to you: all that matters is to look at the "form" of the solution, and then check the C++ code that follows to see how simple and similar it is]

1. construct the $m \times n$ proximity matrix $G$ with elements \[ g_{ij} = \exp(-d_{ij}^2 / 2\sigma^2), \] where $\sigma$ is a scale parameter
2. perform singular value decomposition of $G$ \[ G = U S V', \] where $U, V$ are orthogonal $m \times m$, $n \times n$ matrices respectively, and $S$ is a non-negative diagonal $m \times n$ matrix
3. replace each diagonal element $s_{ij}$ of $S$ by $1$ into a new $m \times n$ matrix $E$, and reconstruct \[ P = U E V' \]
4. finally, map point $a_i$ to $b_j$ if element $p_{ij}$ of $P$ is the greatest element of row $i$ and column $j$ of $P$

the code

Ok, and here goes the actual code that computes all this in practice. The following is a function that takes as input the $(x,y)$ coordinates of the two point sets $a_i, b_j$ along with parameter $\sigma$, and computes a mapping from points $a_i$ to $b_j$ and its inverse. For those familiar with the Matlab syntax, we give the code for both ivl C++ (left) and Matlab (right):

Certainly, the ivl code looks more like Matlab [even if you are not familiar] than C++. However, we do have to declare all variables in C++ whereas in Matlab declarations are not needed and types are determined automatically. Also, array indices begin at 0 in C++ and 1 in Matlab [line 25]. But let us look in more detail at the new elements of syntax brought into C++ by ivl.

the unveiling

arrays	array array_2d	There are one-dimensional arrays [class array [lines 2-4,20,24]] in ivl, as well as two-dimensional [class array_2d [line 6]]. Template parameter T is the data type and could be float or double in our function; in general, it could be a primitive type like int or bool, or any user-defined, composite type. For instance, std::complex or even other containers like array or std::vector.
tuples	tuple (_,a,b)	There are tuples [class tuple], implicitly constructed e.g. by syntax (_,a,b), representing a pair of elements $(a,b)$. A tuple can have an arbitrary number of elements of arbitrary types, whereas all elements of an array have the same type.
multiple return arguments	ret	In turn, tuples are used to return multiple arguments from functions, like max [lines 21,22], meshgrid [lines 9,10], or even our own function here. Class ret inherits tuple and makes sure that no copies take place on return.
output argument overloading	max++ meshgrid++	More than that, ivl supports output argument overloading: by default, max just returns the maximum element of an array, whereas max++ can return the position of this element as well. A different left value triggers a different operation, and this is resolved statically by the compiler.
element-wise expressions	g=exp(-d->*2)	Arrays can be combined with element-wise functions and operators to form expressions, in turn assigned to another array [lines 12, 14]. Most STL functions and C++ operators are so extended for arrays in ivl. This includes logical operators as well [lines 17,25].
lazy evaluation		What is more interesting, actual evaluation does not take place before assignment. In effect, the compiler constructs the corresponding expression for the elements of the arrays, and then a single for loop executes at runtime, eliminating all temporary objects.
linear algebra ivl-lina	svd++	Singular value decomposition is computed in module ivl-lina by template function svd [line 16], which actually wraps different versions of the corresponding function of LAPACK, using the underlying allocated memory of the ivl arrays involved, without input/output copying. Most common linear algebra operations are supported this way.
matrix expressions	a()*b() !a()	Given an array a, expression a() gives access to additional operators. In particular, two-dimensional arrays are seen as matrices, conveniently supporting matrix multiplication, left/right division, exponentiation, and [conjugate] transpose [line 18].
scalars	_[a] a->*n	The exponentiation operator ->* can be applied to arrays, matrices, but also to scalars [class scalar] of primitive types like double when enclosed by _[] [line 14]. The same syntax is used for several more advanced operations, when the scalar data type is e.g. an array, a class, or a function.
optional arguments	f(x,_,z)	The underscore character _ is heavily [ab]used in ivl for several different purposes. One more is to denote an empty array [of any type]. Resembling a place holder, this represents a missing input argument at any position [lines 21,22], in contrast to optional arguments of C++ that typically lead to ambiguities unless they appear last.
ranges	(a,_,b)	Resembling an ellipsis, yet another use for _ is to construct a range [class range [line 25]]: syntax (a,_,b) represents a range of [integer or floating] numbers from a to b with step 1, which can also be seen as an array but without that much allocated space.

the moral

You may think that ivl has everything that Matlab has. Well, not even close to what Matlab had back in 1990. But it does have most elements of Matlab language syntax that are missing from C++. And it has a lot more advanced features, e.g. different types of views and iterators, array operations on class members, function objects and dynamic multithreading. Combined with C++ type checking, class hierarchies, templates, inlining and compiler optimization, these provide a powerful development environment.